Реализация алгоритма
Дерево отрезков
храним в массиве SegTree длины 4*MAX, где MAX –
максимальное количество элементов, которое может храниться в отрезке. Структура
node хранит минимальное min и максимальное max значение на отрезке.
#define MAX 100000
struct node
{
int min, max;
} SegmentTree[4*MAX];
На вход
процедуре build построения дерева отрезков передается массив a, номер текущей
вершины дерева Vertex и границы
отрезка Left и Right, соответствующие вершине Vertex.
void BuildTree(int
*a, int Vertex, int
Left, int Right)
{
if (Left ==
Right)
SegmentTree[Vertex].min =
SegmentTree[Vertex].max = a[Left];
else
{
int Middle
= (Left + Right) / 2;
BuildTree(a, 2*Vertex, Left, Middle);
BuildTree(a, 2*Vertex+1, Middle+1, Right);
Пересчитываем минимальное и
максимальное значение на отрезке [Left, Right], используя информацию сыновей
вершины Vertex.
SegmentTree[Vertex].min =
min(SegmentTree[2*Vertex].min,SegmentTree[2*Vertex+1].min);
SegmentTree[Vertex].max =
max(SegmentTree[2*Vertex].max,SegmentTree[2*Vertex+1].max);
}
}
Вершине Vertex соответствует отрезок [LeftPos; RightPos]. Функция GetMin возвращает минимум на отрезке [Left; Right].
int GetMin(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right)
{
if (Left >
Right) return INF;
if ((Left ==
LeftPos) && (Right == RightPos))
return
SegmentTree[Vertex].min;
int Middle =
(LeftPos + RightPos) / 2;
return
min(GetMin(2*Vertex, LeftPos, Middle, Left, min(Right,Middle)),
GetMin(2*Vertex+1, Middle+1, RightPos,
max(Left,Middle+1),Right));
}
Вершине Vertex соответствует
отрезок [LeftPos; RightPos]. Функция GetMax возвращает
максимум на отрезке [Left; Right].
int GetMax(int
Vertex, int LeftPos, int
RightPos, int Left, int
Right)
{
if (Left >
Right) return -INF;
if ((Left ==
LeftPos) && (Right == RightPos))
return
SegmentTree[Vertex].max;
int Middle =
(LeftPos + RightPos) / 2;
return
max(GetMax(2*Vertex, LeftPos, Middle, Left, min(Right,Middle)),
GetMax(2*Vertex+1, Middle+1,
RightPos, max(Left,Middle+1),Right));
}
Вершине Vertex соответствует
отрезок [LeftPos; RightPos]. Функция Update присваивает
элементу с индексом Position значение
NewValue.
void Update(int
Vertex, int LeftPos, int
RightPos,
int
Position, int NewValue)
{
Если вершине Vertex
соответствует отрезок, состоящий из одного элемента (LeftPos равно RightPos),
то мы дошли до листа дерева отрезков. Минимум и максимум на отрезке, состоящего
из одного элемента, равен NewValue.
if (LeftPos == RightPos)
SegmentTree[Vertex].min =
SegmentTree[Vertex].max = NewValue;
else
{
Иначе вычисляем, в каком – левом или
правом сыне вершины Vertex лежит элемент с индексом Position. Запускаем рекурсивно его модификацию.
int Middle
= (LeftPos + RightPos) / 2;
if
(Position <= Middle)
Update (2*Vertex, LeftPos, Middle,
Position, NewValue);
else
Update (2*Vertex+1, Middle+1, RightPos,
Position, NewValue);
Пересчитываем значение минимума min
и максимума max в текущей вершине Vertex дерева отрезков.
SegmentTree[Vertex].min =
min(SegmentTree[2*Vertex].min,SegmentTree[2*Vertex+1].min);
SegmentTree[Vertex].max =
max(SegmentTree[2*Vertex].max,SegmentTree[2*Vertex+1].max);
}
}
Основная часть программы. Генерируем
последовательность ai
согласно приведенной в условии задаче формуле. Последовательность храним в
массиве int a[MAX+1];
for(i = 0; i
<= MAX; i++)
a[i] = (i * i) % 12345 + ((i * i) % 23456 *
i) % 23456;
Строим дерево отрезков.
BuildTree(a,1,0,MAX);
Читаем входные данные и отвечаем на
запросы.
scanf("%d",&k);
while(k--)
{
scanf("%d
%d",&x,&y);
if (x > 0)
printf("%d\n",GetMax(1,0,MAX,x,y) -
GetMin(1,0,MAX,x,y));
else Update(1,0,MAX,-x,y);
}
Вторая реализация при помощи
массива
Обозначим через INF плюс бесконечность.
#define INF 2000000000
Дерево отрезков будем хранить в виде
кучи в ячейках v[1]..v[2*n], всего 2
* n – 1 элементов. Сыновьями вершины v[i] будут v[2*i] и v[2*i + 1]. Функция BuildTree
строит дерево отрезков из элементов вектора a. Поскольку в каждой вершине
дерева требуется поддерживать минимум и максимум на отрезке, то элементом v[i] будет пара
целых чисел. Первое число пары соответствует минимуму, а второе максимуму на
отрезке.
void BuildTree(vector<pair<int,int> >
&a)
{
Увеличим размер массива n до степени двойки, введя фиктивные
вершины.
int i, n = (1
<< (int)(log(1.0*(a.size() -
1))/log(2.0)) + 1);
a.resize(2*n, make_pair(INF,0));
for(i = n ; i
< 2 * n; i++) a[i] = a[i - n];
for (i = n -
1; i > 0; i--)
a[i].first
= min(a[2 * i].first, a[2 * i + 1].first),
a[i].second = max(a[2 * i].second, a[2 * i
+ 1].second);
}
Функция MinMax вычисляет максимум и минимум на отрезке.
Возвращает их разность.
int MinMax(vector<pair<int,int>
>&v, int l, int
r)
{
int minRes =
INF, maxRes = -INF;
int n =
v.size() / 2;
l += n - 1, r += n - 1;
while (l
<= r)
{
Если l – правый сын своего родителя, то учитываем его фундаментальный
отрезок.
if (l &
1)
minRes = min(minRes, v[l].first),
maxRes = max(maxRes, v[l].second);
Если r – левый сын своего родителя, то учитываем его фундаментальный
отрезок.
if (!(r
& 1))
minRes = min(minRes, v[r].first),
maxRes = max(maxRes, v[r].second);
Сдвигаем указатели на уровень выше.
l = (l + 1) / 2, r = (r - 1) / 2;
}
return maxRes
- minRes;
}
Присвоим i-ому
элементу массива значение x.
void update(vector<pair<int,int>
>&v, int i, int
x)
{
int n =
v.size() / 2;
i += n - 1;
Присваиваем значение x листу.
v[i] = make_pair(x,x);
Двигаемся от листа к корню,
пересчитываем значения минимумов и максимумов. Отцом вершины i является вершина 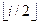 .
.
while (i /=
2)
v[i].first
= min(v[2 * i].first, v[2 * i + 1].first),
v[i].second = max(v[2 * i].second, v[2 * i
+ 1].second);
}
Основная часть программы. Генерируем последовательность ai согласно приведенной в
условии задаче формуле и заносим ее в вектор v.
vector<pair<int,int> > v;
for(i = 1; i <= 100000; i++)
{
ai = (i * i) % 12345 + ((i * i) % 23456 * i)
% 23456;
v.push_back(make_pair(ai,ai));
}
Строим дерево отрезков.
BuildTree(v);
Читаем входные данные и отвечаем на запросы.
scanf("%d",&k);
while(k--)
{
scanf("%d
%d",&x,&y);
if (x > 0)
printf("%d\n",MinMax(v,x,y));
else
update(v,-x,y);
}


